目 次
研修を終えて
企画情報班
平成11年度の防災研技術室研修会も、ほぼ日程どうり実施出来、充実した2日間でありました。鳥取観測所の技官をはじめ、関係施設の方々には全面的に協力をしていただきお礼を申し上げます。
これまで、分野の違った隔地施設での研修を一通り行ってきて、技官各位が隔地勤務の難しさ、少人数での厳しさ等を感じ取って戴いたことと思います。今後の研修につきましては、以前のアンケート調査をも参考にし、研修内容、場所など一度原点に戻り、白紙から考え直してはと感じております。
研修についてのご意見をお聞かせ願って参考にしたいと思います。
* 京大総合技術部の研修受講者名を、鳥取研修において読み上げましたが当日欠席者も有り再度報告いたします。
受講者名(敬称略)
第23回 平成12年2月 近藤・内山・藤原・多河・志田
第24回 平成12年7月 矢部・平野・羽野・杉政・松尾
第25回 平成13年2月 中川・浅田・藤木・河内・園田保
次回(11月中旬)は、多河・平野両技官にお願いします。
TOP
惑星の運動-簡単なアニメーション
藤 原 清 司
1.はじめに
先月号に続いて星の話だが、真似をした訳ではない。数年前に、宇治川水理実験所で教官と技官数名のグループで勉強会を開いていたときに、自分で作った「惑星の運動-簡単なアニメーション」のプログラムの紹介をしようと思ったのである。従って、その時の勉強会のメンバーには二番煎じになるがお許しいただきたい。
このプログラムで使っているアルゴリズムは私のオリジナルではない。有名なファインマン先生の物理の教科書(ファインマン物理学Ⅰ 力学 坪井忠二訳 岩波書店, P.122-P.134)に載っているものを、そのままプログラミングしたのである。初学者にとって適当な数値解法の解説であると思われるこの章には、最初にバネの運動方程式の数値解法の話があり、次に惑星の運動の数値解法について述べられている。
この本を読んだときに最初フォートランでプログラムを作り、ミニコンのプロッターに惑星軌道の絵を描かせて遊んでいた。数年して、上記の勉強会でマイクロソフト社のクイックベーシック(QB)を集中的に学び、パソコンのディスプレイ上で簡単にグラフィックスが実現できることが分かり、再度、フォートランのプログラムをクイックベーシックに書き直してさらに簡単なアニメーションにすることにした。
ファインマン先生の教科書には、太陽と周りの水星、金星、地球など太陽系全体の運動方程式の数値解法についても言及してあるが、それはとてもプログラムが煩雑になりそうなので、惑星1個の場合について解説してある部分をそのままプログラミングすることにした。
2.プログラミングの基礎
ファインマン先生の教科書に従って順に解説を進めていくと、最初に、計算を簡単にするために、二次元平面の座標原点に太陽を置いて動かないものと仮定した上で、ニュートンの運動法則と万有引力の法則から惑星のx方向とy方向の加速度を求める。
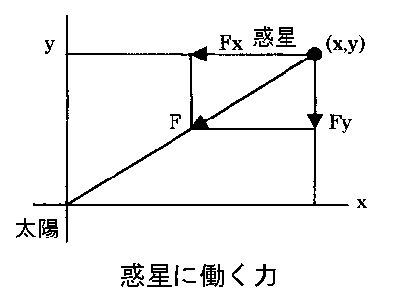 次図において、rを動径、Gを万有引力定数、Mを太陽の質量、mを惑星の質量とすると、大と小の二つの三角形は相似であるから力のx方向成分の全体の力に対する割合は、
次図において、rを動径、Gを万有引力定数、Mを太陽の質量、mを惑星の質量とすると、大と小の二つの三角形は相似であるから力のx方向成分の全体の力に対する割合は、
-Fx/|F| = x /r ここで 、|F| = GMm/r2
である。ゆえに、
Fx = -|F|x/r = -GMmx/r3
また、一般に F = ma = m(dv/dt) だから、
m(dvx/dt) = -GMmx/r3
ここで、GM = 1 と仮定して
dvx/dt -= -x/r3
一方、y方向も同様にして、
dvy/dt = -y/r3
と求まる。
3.計算の考え方
いま、与えられた時刻 t に、物体の位置は S で速度は Vs であるとする。時間が少したって時刻が (t+Δt) になったとき、物体の位置は何で速度は何であるか。任意の時刻 t においてΔt が小さいとすれば、t における物体の位置と速度から時刻 (t+Δt) における物体の位置を、次のように求めることができる。位置 S は、
S(t+Δt) = S(t)+Δt・Vs(t)
である。さらに、時刻 (t+Δt) における物体の速度を求めるには、時刻 t における物体の速度と、前述のように運動法則から物体の加速度 as(t) を導いて、
Vs(t+Δt) = Vs(t)+Δt・as(t)
とする。すでにお分かりのように、Δt が小さければ小さいほどこれらの式は精確になる。
以上は一般的な考え方だが、惑星の運動の場合には、前述の計算結果に基づき上式を x成分と y成分とに分けて、さらに、計算の精度を上げるために少し工夫して以下のようにする。
ただし、Δt は時間刻みの量、t は t = 0 からの経過時間、x は太陽を原点としたときの惑星の x座標、y は同じく y座標、ax は x方向の加速度、ay は y方向の加速度、r は太陽と惑星との距離である。
《 x方向の方程式 》
x(t+Δt)- = x(t)+Δt・Vx(t+Δt/2)
Vx(t+Δt/2) = Vx(t-Δt/2)+Δt・ax(t)
特に最初だけ、 Vx(Δt/2) = Vx(0)+(Δt/2)・ax(0)
ax(t) = -x(t)/{r(t)}3
《 y方向の方程式 》
y(t+Δt)- = y(t)+Δt・Vy(t+Δt/2)
Vy(t+Δt/2) = Vy(t-Δt/2)+Δt・ay(t)
x方向と同様に特に最初だけ、 Vy(Δt/2) = Vy(0)+(Δt/2)・ay(0)
ay(t) = -y(t)/{r(t)}3
《 距離の方程式 》
r(t) = √{x(t)}2+{y(t)}2 ( 注:根号は {y(t)}2 までつづく )
上式において、最初にΔt の大きさと惑星の x方向の位置と速さ、y方向の位置と速さが与えられている。それを出発点として、x、y、ax、ay、r については t = 0 から始めて t = Δt, 2Δt, 3Δt…と計算し、Vx, Vyについては最初だけ特別の式を使い、次から t = Δt, 2Δt, 3Δt…と計算を続ける。
以上のように、プログラムの構造としては単純な計算の繰り返しである。
4.フローチャート
次に、フローチャートを示す。
5.おわりに
プログラムに採用した初期条件は、ファインマン先生の教科書そのままである。本文にも書いたが、Δtが小さければ小さいほどこのプログラムは精確になるが、無限小にはできない。その結果、惑星軌道が最初の位置よりだんだんずれてくる。このプログラムでは、楕円軌道が右回りにずれてくる(僅少!)。それも見ていて、実際の惑星軌道においても近日点の位置がずれていくという現象があるので、それを模擬しているようでおもしろい。また、当たり前だろうけど、惑星の動きが太陽に遠くなれば遅くなり、近くなれば速くなるというケプラーの面積速度保存の法則を忠実に再現していておもしろい。こんなおもちゃのようなプログラムで、広大無辺な宇宙の動きがたとえ一部でも目の当たりにできるとは驚きである。少々大げさかも知れないが、ニュートン力学の偉大さを見せつけられる思いがする。かくなる上は、太陽系(ソーラシステム)全体のアニメーションを作りたいのだが、最初にも言ったようにプログラミングが非常に煩雑になりそうなので(単純ではあるが、しちめんどうな連立方程式を計算しなければいけない!)、恐れをなしてまだその気力が涌かない。
もし、読者でこの記事に興味を持たれた方がおられたなら(似たようなものを、すでに試みられた方もおられるかも知れませんが)、一度プログラミングされて(クイックベーシックのソフトがなくても、適当な言語に翻案されて)いろいろに試されると面白いのではないかと思う。ひよっとして、何か新しい発見があるかも知れない。
ところでこの間、ある本*を読んでいたら、惑星の運動について計算誤差をより少なくするための、ファインマン先生とは少し違ったアルゴリズムが載っていた。基本的な部分はあまり変えようがないと思うが、より速くて精確なアルゴリズムを自分で考案してみたらどうだろう。そして、すてきなプログラム(例えば、惑星が複数個存在した場合や衛星が存在した場合などの)ができたときには、是非私までご一報ください。
それでは最後に、プログラムを付記して終わります。
―――《 プログラム 》―――
DECLARE SUB Animation (xx!, yy!)
DECLARE SUB CountN (x!, y!, k%)
DECLARE SUB GraphMode ()
DECLARE SUB Initial ()
DECLARE SUB Count0 (x!, y!)
DECLARE SUB Count1 (x!, y!)
' *************************************
' * 惑星の運動(qwnu.bas) *
' * 1993/7/6 H.Seizi *
' *************************************
'グラフィックス画面の設定
GraphMode
'初期条件の設定
DIM SHARED t!, x0!, y0!, vx0!, vy0!
Initial
'時刻t=0のときの,太陽からの距離及び加速度
DIM SHARED ax0!, ay0!
Count0 Xpoint0!, Ypoint0!
Animation Xpoint0!, Ypoint0!
'時刻t=Δtのときの,太陽からの距離及び加速度
DIM SHARED x1!, y1!, vx1!, vy1!, ax1!, ay1!
Count1 Xpoint1!, Ypoint1!
Animation Xpoint1!, Ypoint1!
'時刻t=2Δt,3Δt・・・のときの,太陽からの距離及び加速度
VIEW PRINT 1 TO 3
n% = 0
DO
n% = n% + 1
CountN XpointN!, YpointN!, n%
Animation XpointN!, YpointN!
PRINT USING "時刻 t の値は, t=####.#"; t3!
PRINT "惑星の現在位置は,x="; XpointN!, "y="; YpointN!; " "
LOOP WHILE INKEY$ = ""
'画面の初期化
VIEW PRINT: CLS 0
END
'***********************************************************
'惑星のアニメーション
SUB Animation (xx!, yy!)
FOR m% = 1 TO 8
CIRCLE (xx!, yy!), .02, 2
PAINT (xx!, yy!), 2, 2
NEXT m%
FOR m% = 1 TO 5
CIRCLE (xx!, yy!), .02, 1
PAINT (xx!, yy!), 1, 1
NEXT m%
END SUB
'************************************************
'時刻 t=0 のときの,太陽からの距離及び加速度
SUB Count0 (x!, y!)
r01! = SQR(x0! ^ 2 + y0! ^ 2)
r02! = 1 / r01! ^ 3
ax0! = -x0! * r02!: ay0! = -y0! * r02!
x! = x0!: y! = y0!
' PRINT
' PRINT " T X VX AX Y VY AY R 1/R^3"
' PRINT USING " 0.00 ###.### ###.### ###.### ###.### ###.### ###.###"; x0!; ax0!; y0!; ay0!; r01!; r02!
END SUB
'************************************************
'時刻 t=Δt のときの,太陽からの距離及び加速度
SUB Count1 (x!, y!)
vx1! = vx0! + t! / 2 * ax0!: vy1! = vy0! + t! / 2 * ay0!
x1! = x0! + t! * vx1!: y1! = y0! + t! * vy1!
r11! = SQR(x1! ^ 2 + y1! ^ 2)
r12! = 1 / r11! ^ 3
ax1! = -x1! * r12!: ay1! = -y1! * r12!
t1! = t! / 2
x! = x1!: y! = y1!
' PRINT USING "##.## ###.### ###.###"; t1!; vx1!; vy1!
' PRINT USING "##.## ###.### ###.### ###.### ###.### ###.### ###.###"; t!; x1!; ax1!; y1!; ay1!; r11!; r12!
END SUB
'************************************************
'時刻 t=2Δt,3Δt・・・ のときの,太陽からの距離及び加速度
SUB CountN (x!, y!, k%)
SHARED t3!
vxn! = vx1! + t! * ax1!: vyn! = vy1! + t! * ay1!
xn! = x1! + t! * vxn!: yn! = y1! + t! * vyn!
rn1! = SQR(xn! ^ 2 + yn! ^ 2)
rn2! = 1 / rn1! ^ 3
axn! = -xn! * rn2!: ayn! = -yn! * rn2!
x1! = xn!: y1! = yn!
vx1! = vxn!: vy1! = vyn!
ax1! = axn!: ay1! = ayn!
t2! = t! * (k% + 1 / 2)
t3! = t! * (k% + 1)
x! = xn!: y! = yn!
' PRINT USING "##.## ###.### ###.###"; t2!; vxn!; vyn!
' PRINT USING "##.## ###.### ###.### ###.### ###.### ###.### ###.###"; t3!; xn!; axn!; yn!; ayn!; rn1!; rn2!
' IF k% MOD 5 = 4 THEN
' PRINT " -----+-------+-------+-------+-------+-------+-------+-------+-------"
' END IF
END SUB
'************************************************
'グラフィックス画面の設定
SUB GraphMode
SCREEN 0
CLS 0
VIEW (169, 49)-(469, 349), 1
WINDOW (-1.5, -1.5)-(1.5, 1.5)
LINE (-1.5, -1.5)-(1.5, 1.5), , B
LINE (-1.5, 0)-(1.5, 0)
LINE (0, -1.5)-(0, 1.5)
FOR i! = -1 TO 1 STEP .5
IF i! <> 0 THEN
LINE (-1.5, i!)-(1.5, i!), 3
LINE (i!, -1.5)-(i!, 1.5), 3
END IF
NEXT i!
CIRCLE (0, 0), .1, 5
PAINT (0, 0), 5, 5
END SUB
'************************************************
'初期条件の設定
SUB Initial
t! = .1
x0! = .5: y0! = 0
vx0! = 0: vy0! = 1.63
END SUB
―――――― ◇ ――――――
*)「計算物理の世界」:大西楢平ほか3名、共立出版、1998。
TOP
可搬型衛星地震観測装置のセッティング
技術室 小泉 誠
まえがき
1996年から97年にかけて通信衛星を用いた地震観測テレメタリングシステムが全国一斉に導入された。これに伴い地震予知研究センターでも定常地震観測点および臨時地震観測点で衛星地震テレメータが使われるようになった。臨時地震観測としては97年の大学合同観測において東北地方で使われ、今年は北海道で現在稼働している。そこでこれまでその設置に携わった経験からたいへんローカルな話で恐縮だが、日頃気づいていること、注意すべきことについて少し紹介し、「技術室通信」一回分の義務を果たそうという魂胆である。観測装置の設置と稼働方法については分厚いマニュアルに詳しく書かれているのでここで説明するつもりはない。
(写真)衛星アンテナの設置例
 可搬型衛星地震観測装置のアンテナは写真に示すようなもので、アンテナ直径0.75mの場合そのベース部は142kgにもなる。文字通り可搬型なので特製の収納鞄が幾つも用意されていて背負う事が出来るが、幸いまだ担いだ経験はないし今後も経験したくはない。設置には車を使って運ぶしか手はなく、電車やバスを乗り継いで行くわけにもいかない。測器の構成はベース部を含みオフセットパラボラアンテナと、焦点に取り付けられたODU(Outdoor Unit、送受信機に相当)と、室内に置かれるIDU(Indoor Unit、衛星回線のモデムに相当)からなっている。ベース部は土の上やコンクリート上に置かれる。写真は畑の中に置いた例で、風などに対して回転が起こらぬようパイプを打ち込んで補強している。アンテナの高さは雪の多いところでは高くしている。因みに今年は台風の影響で西日本、特に九州で衛星アンテナの被害が続出した。
可搬型衛星地震観測装置のアンテナは写真に示すようなもので、アンテナ直径0.75mの場合そのベース部は142kgにもなる。文字通り可搬型なので特製の収納鞄が幾つも用意されていて背負う事が出来るが、幸いまだ担いだ経験はないし今後も経験したくはない。設置には車を使って運ぶしか手はなく、電車やバスを乗り継いで行くわけにもいかない。測器の構成はベース部を含みオフセットパラボラアンテナと、焦点に取り付けられたODU(Outdoor Unit、送受信機に相当)と、室内に置かれるIDU(Indoor Unit、衛星回線のモデムに相当)からなっている。ベース部は土の上やコンクリート上に置かれる。写真は畑の中に置いた例で、風などに対して回転が起こらぬようパイプを打ち込んで補強している。アンテナの高さは雪の多いところでは高くしている。因みに今年は台風の影響で西日本、特に九州で衛星アンテナの被害が続出した。
1.通信衛星
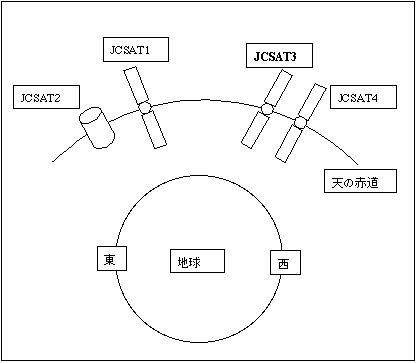
図1に示すように南から少し西にある通信衛星JSAT3は、1995年8月に打ち上げられたもので、東経128度の赤道上空35,800kmにある静止衛星である。Sky PerfecTVでお馴染みのディジタル多チャンネル放送の商用通信衛星である。映像だけでなく大量のマルチメディア情報を扱うことが出来る衛星で、比較的小さな口径のアンテナでデータの送受信ができるKu帯(12GHz付近の周波数)を地震観測では利用している。(株)日本サテライトシステムズが運営している。
因みに通信衛星を用いた地震観測テレメタリングシステム(全国国立大学)の中継局でお世話になっているSNET群馬通信センター(株・衛星ネットワーク)は第二種電気通信事業者としてこの衛星を利用したサービスを展開している。このSNETさんとは設置に際して必ず連絡を取りながらアンテナの調整を行なわねばならない。
 |
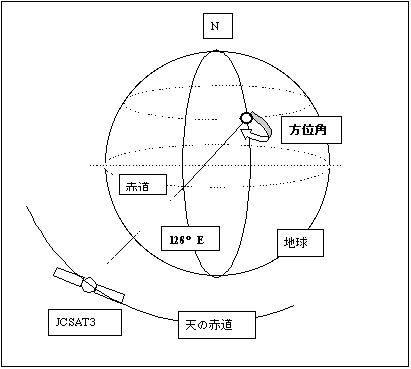 |
| (図1)JCSAT衛星の位置 | (図2)方位角 |
2.パラボラアンテナの設置
アンテナは地面が固く平らである所に置くことが重要である。もちろん電磁波を遮る木や建物がないことは当然であるが、木が小さくても成長が非常に早いので注意が必要である。観測点の設置には土地や建物の使用許可を得るべく事前に調査と交渉のため前もって下見に出かけるが、必ずアンテナを想定した上見が下見より大切である。
まず、アンテナ面を指定された方位角に向けなければいけない。図2のようにある観測地点(○印)から見た東経128度方向を北から時計回りに測った角度を方位角(AZ)として向けてあげる。マニュアルには定常観測点(ルーティン点)の緯度・経度・方位・仰角などが書かれているが、これから新たに設置しようとする場所については自分で求めなければならない。しかし正確な方位角の求め方は単に緯度・経度の差から出せるのか私はこの辺りを知らない。難しい式があるのかもしれない。この場合注意することは、北からの方位角が真の北なのか磁北なのかをはっきりさせておかねばならない。方位を出す時はパラボラアンテナの柱(ポールマウント部)に細い紐を結びつけ、クリノメータを用いてその方位に紐を長く引っ張ってアンテナ面の方向を調整している。クリノメータを使う時は近くに鉄製のものがないこと、地中にもないことに注意することである。今年の北海道のある臨時観測点では岩盤が露出しており、それに鉄分が含まれていたことで方位を出すのにたいへん苦労した。アンテナのお皿は丸いので目視で慎重に合わせることが大切である。
次は仰角(ギョウカク、ELとも呼ぶ)の設定である。仰角とは図3で書いたように、いま設置しようとしている場所を○印で表すと(この例では北半球で約30数度の緯度の場所)、この地点の地平線と通信衛星JSAT3を結んで出来る角度である。従って高緯度地方へ行くほどこの仰角は小さくなる。各地の仰角は方位角同様、定常観測点についてはマニュアルに書いてあるが、臨時観測点の設置の場合は自分で求めなければならない。しかし方位角に比べると角度の範囲が狭く、設定は仰角が目盛られたケガキ線に合わせて仰角調整ネジ(4本)を締め付けた後、微調整ネジを使って調整する。ベース部が水平に保たれていればこの目盛りはかなり正確である。ただこの微調整機構は構造的に無理があり、ネジを大きく回しすぎるとアンテナの重みがかかり過ぎて金具を曲げてしまう危険があり、あくまで補助的に使うことが大事である。
最後にV偏波角の調整であるが、これもマニュアルに書いてあるので時計回りに指定された角度に合わせる。最終的には中継局とのやりとりで決められる。
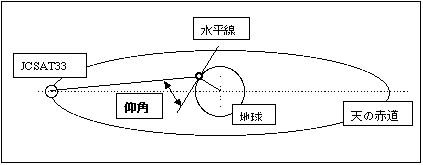 |
| (図3)仰角 |
3.クリノメータの精度について
衛星観測装置の設置に何回か携わっているが、正確な方位を出すことにいつも苦労している。いつも方位の決定に用いるクリノメータは小さいもので(図4)、地学観察に使われているものである。コンパスを使用すれば精度がでるのかもしれないが手軽なので使っている。長辺僅か11cm、方位の目盛り直径4cm足らずのガラス窓に360度の目盛りのあるクリノメータでは方位の読取りには数度の誤差が発生するだろう。またクリノメータ自体の方位を指す精度もそれほど良くないかもしれない。つね日頃疑問に思っていたので調べてみた。たくさんのクリノメータをお借り出来る機会があり測定を行った。表1はその時のデータである。この時比較に用いたコンパスは三脚付の古いものであるが、目盛り盤は直径9.5cmあり、読み取り誤差はクリノメータに比べ格段に良いものである。測定は宇治構内のクレーテニスコート内で周りに鉄製のものがないことを確認し、任意の方向に約10m程度細い紐を張り、同じ地点にクリノメータをおいて方位を読みとった。一個の不良品(針がどこでも止まった)を除いて、N5°WからN10°Wの範囲内であった。このうち5°と10°を除けば9割方、7°から8°の物が多かった。この結果からクリノメータの個体のばらつきは比較的小さいことがわかる。一方、コンパスの精度は一台だけではわからないが、この時N5°Wでほぼ正確な値を示していると仮定すれば、クリノメータの方位精度は±3°位の範囲内にあるのではないかと思われる。JSAT3の方位のごく近辺(約4度東)に他の衛星(NSTAR)があると聞いているが、このクリノメータの精度からあまり神経質になって方位求めても無駄なのかもしれない。
(表)1 測定値一覧
| クリノメータ ナンバー | 指示方位 | クリノメータ ナンバー | 指示方位 | 備 考 |
| 23 | N8°W | 58 | N7°W | 測定日:1999/10/8 |
| 44 | 8 | 61 | 10 | クリノメータ:Showa Sokki Co |
| 45 | 7 | 62 | 7 | 天候:曇り、無風 |
| 46 | 7 | 63 | 7 | 場所:宇治テニスコート内 |
| 47 | 7 | 64 | 5 | 比較に用いたコンパス: |
| 48 | 7 | 65 | 7 | 測器社製,No16072 |
| 49 | 7 | 66 | 7 | 指示方位=N5°W |
| 50 | 8 | 67 | 7 | |
| 51 | 7 | 70 | 8 | |
| 52 | 8 | 72 | 7 | |
| 53 | 7 | 73 | 2 | No.73は不良品 |
| 54 | 9 | 75 | 6 | |
| 55 | 7 | 76 | 7 | |
| 56 | 7 | 77 | 7 | |
図4.実物大のクリノメータ
 4.屋内装置
4.屋内装置
衛星アンテナの方位と仰角が確定したらレベルチェッカーを使って受信レベルを測定する。14番のトランスポンダのTV信号で1223MHzのV偏波のみを受信することで代表できる。レベル値は65dBμ以上(ケーブル長50mの時)が受信出来る様アンテナの方位・仰角を再調整する。レベルチェッカーはIDUのTVout端子から信号を受けるが、この時レベルチェッカーのDC電源供給スイッチは必ずOFFにすること。ONにするとIDUを壊すので注意が要る。
受信レベルが所定の値に達したらここからはUAT(User Access Test)の手順に基づいて進み、IDUの立ち上げとINIT SG(Initial System Generation)の設定に入る。ここでの注意は、この装置のキーに癖があり押し方によって(長く押すと2ステップ飛ぶことがある)入力がうまく行かないことがある。覚えておいて損はない。中継局である(株)SNETと電話でやりとりしながら行うが、携帯電話が通じないときは携帯型衛星電話が必要となる。
IDUのリアルタイム画面遷移は,
OFF LINE→OB OPEN(下り回線)→OB SYNC(同期)→IB OPEN(上り回線)
→ON LINEと変わっていくが、IB OPEN とON LINEの間にREADING SG、 READING PRM 、 LOADING PGM、 RAM RUNなどのステップが入ってくる。アンテナの向きが良好でない場合や回線状態が悪いときはこのステップが何回か繰り返されることがあり、 ON LINEまで時間がかかる。正常に推移したときでも30分から1時間程度かかる。もちろんOFF LINEで繋がらないこともある。
あとがき
断片的に書いたつもりが長々と内容の乏しいものになってしまった。全てはマニュアルをしっかり読んで実際の設置に望んでほしい。リアルタイム画面遷移については私はまだよく分かっていない。詳しい方がおられたら教えてほしいと思っている。
TOP
dptech@adm99.dpri.kyoto-u.ac.jp
技術室通信に戻る


 次図において、rを動径、Gを万有引力定数、Mを太陽の質量、mを惑星の質量とすると、大と小の二つの三角形は相似であるから力のx方向成分の全体の力に対する割合は、
次図において、rを動径、Gを万有引力定数、Mを太陽の質量、mを惑星の質量とすると、大と小の二つの三角形は相似であるから力のx方向成分の全体の力に対する割合は、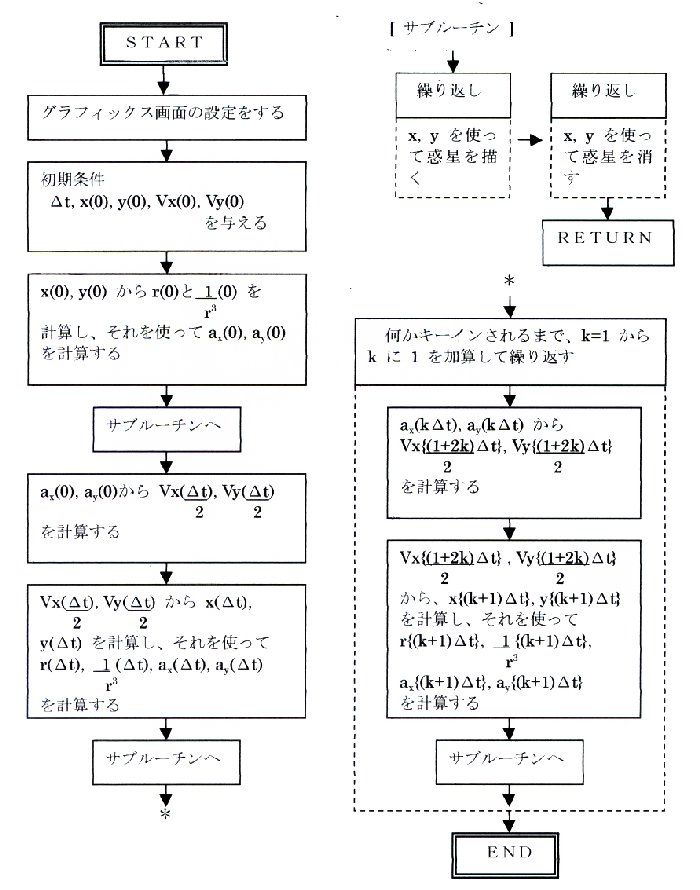
 可搬型衛星地震観測装置のアンテナは写真に示すようなもので、アンテナ直径0.75mの場合そのベース部は142kgにもなる。文字通り可搬型なので特製の収納鞄が幾つも用意されていて背負う事が出来るが、幸いまだ担いだ経験はないし今後も経験したくはない。設置には車を使って運ぶしか手はなく、電車やバスを乗り継いで行くわけにもいかない。測器の構成はベース部を含みオフセットパラボラアンテナと、焦点に取り付けられたODU(Outdoor Unit、送受信機に相当)と、室内に置かれるIDU(Indoor Unit、衛星回線のモデムに相当)からなっている。ベース部は土の上やコンクリート上に置かれる。写真は畑の中に置いた例で、風などに対して回転が起こらぬようパイプを打ち込んで補強している。アンテナの高さは雪の多いところでは高くしている。因みに今年は台風の影響で西日本、特に九州で衛星アンテナの被害が続出した。
可搬型衛星地震観測装置のアンテナは写真に示すようなもので、アンテナ直径0.75mの場合そのベース部は142kgにもなる。文字通り可搬型なので特製の収納鞄が幾つも用意されていて背負う事が出来るが、幸いまだ担いだ経験はないし今後も経験したくはない。設置には車を使って運ぶしか手はなく、電車やバスを乗り継いで行くわけにもいかない。測器の構成はベース部を含みオフセットパラボラアンテナと、焦点に取り付けられたODU(Outdoor Unit、送受信機に相当)と、室内に置かれるIDU(Indoor Unit、衛星回線のモデムに相当)からなっている。ベース部は土の上やコンクリート上に置かれる。写真は畑の中に置いた例で、風などに対して回転が起こらぬようパイプを打ち込んで補強している。アンテナの高さは雪の多いところでは高くしている。因みに今年は台風の影響で西日本、特に九州で衛星アンテナの被害が続出した。


 4.屋内装置
4.屋内装置